U-value, R-value and λ-value – A brief explaination with Examples
Within energy efficiency an important metric is the thermal transmittance; the U-value. The U-value describes the heat transfer through a construction with a 1 m² surface at a temperature differential of 1 °K. The unit of the U-value is therefore W/(m²K), where W=J/s. The U-value is the sum of the heat transfer by means of radiation, convection and conduction. The purpose of this post is to show how to calculate the U-value in a simple construction as well as explaining the different factors affecting the U-value. The post will not deal with thermal bridges but only constructions using layers of homogenous materials. When calculating the U-value in these constructions there are 3 factors that will affect the U-value. These are:
- 1. The type of material
- 2. The thickness of the material
- 3. The location of the material
1. Material type and λ-value
Beginning with point number 1, the type of material. Different materials are more or less effective at transferring heat. A materials ability to transfer heat is known as its thermal conductivity and is described by its lambda-value, using the Greek letter λ. It is also sometimes referred to as the k-value. The unit of the λ-value is W/mK. It describes the energy transfer int Watt through the material, per meter of material thickness and temperature differential in °K.
Some examples of different λ-value are shown below. The λ-value of materials varies greatly. From the table we can read that the heat transfer through concrete is 42.5 times greater than through mineral wool and for aluminium is 5000 times greater! We can also see that snow can act as effective insulation but due to the great difference between the λ-values of air and water or ice it is important to avoid water to gain access to porous materials as the water replacing air inside the materials pours will degrade the materials insulating properties.
| Construction materials | Example λ-value | Heat transfer compared to mineral wool |
| Mineral wool | 0.04 | 1 |
| Sawdust or wood chips | 0.08 | 2 |
| Wood | 0.12 | 3 |
| Aerated concrete | 0.15 | 3.75 |
| Gypsum board | 0.25 | 6.25 |
| Clay fired brick | 0.60 | 15 |
| Plaster | 1.0 | 25 |
| Glass | 1.0 | 25 |
| Concrete | 1.7 | 42.5 |
| Stone | 3.0 | 75 |
| Stainless steel | 15 | 375 |
| Steel | 50 | 1250 |
| Aluminium | 200 | 5000 |
| Natural materials | Example λ-values | |
| Air | 0.026 | |
| Fluffy snow | 0.05 | |
| Packed snow | 0.60 | |
| Water | 0.60 | |
| Ice | 2.20 |
As a footnote: The values in the table are approximate and more detailed values can often be found from the manufacturer of the material. As an example, new mineral wool can have λ-values of below 0.035 whereas old mineral wool can have values at 0.045 or above. Aerated concrete is possible to get to as low values as 0.04, designed for use in passive houses, but other variants can have a value of 0.2.
2. Material thickness and R-value
The U-value of the material is proportional to the thickness of the material. When the thickness of a material is divided by the λ-value we get the R-value, the thermal resistance. A note is that the R-value of the US-imperial system is not the same as the R-value of the metric system. The unit for the US-imperial system is ft² °F hr/Btu while the unit for the metric system is m² °K/W. To convert the metric R-value to the Imperial R-value, multiply the metric R-value by a factor of 5.682. This post will use the metric R-value which is calculated with the following formula, where d stands for the thickness in meters:
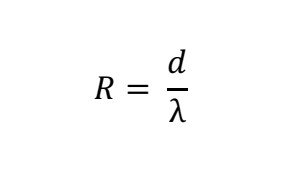
When calculating the R-value of a construction with several layers each layers R-value is calculated separately, and the R-values are then added together to form the total R-value.
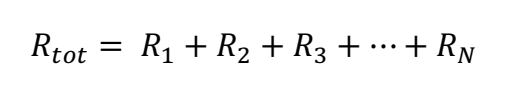
Now follows 2 examples on how to calculate the R-value. Please note that some aspects of calculating the R-value correctly for practical applications are left out and will be explained later. These two examples should therefore not be considered as the correct way to calculate total R-value of the construction, but it is the correct way to calculate the R-value specific to the material layers.
Example 1: Joey have decided to build a garage and as he wants to have the new construction blend with his brick-clad house he has opted to construct the wall out of brick. The wall gets a thickness of 12 cm. What is the R-value?
Answer: 12 cm = 0.12 meters, λbrick = 0.6 W/mK
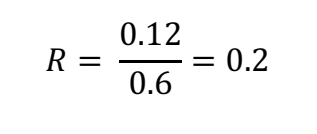
Example 2: Joey is pleased with his new and sturdy brick wall, but he contemplates adding heating to the garage in the future and wants to get an idea on how adding some insulation to the wall would affect the heating cost. What would the R-value become if Joey adds 5 cm of mineral wool to the wall?
Answer: 5 cm = 0.05 meters, λm.wool = 0.04 W/mK
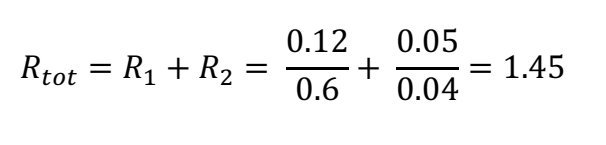
As previously mentioned, when adding additional layers to the construction their insulating properties are added together to form a total R-value.
R-values for practical applications and special R-values
While most R-values are calculated as previously mentioned there are some exceptions. In the table for λ-values Air has a very low value of only 0.026 so one could think that the most effective insulation would be to simply add an airgap inside the wall, the bigger the better. But from experience we know that instead these gaps are filled with insulating materials such as mineral wool. This is because the low value for air is only applicable if the air is still. Inside an airgap the air will always circulate due to convection and thereby transfer heat from the warm side of the airgap to the cold side. The true R-value of the construction becomes dependant on the temperature difference between the two sides of the airgap. This becomes complicated to calculate and therefore airgaps are generally assigned an R-value from a table of practically applicable R-values based on the level of ventilation of the airgap.
Another area which needs to be accounted for by a practical R-value is the external and internal surface resistance. The external and internal surface resistance is applied as a generic value but is reality varying over time. The value for the external resistance can vary greatly with different wind speeds. For simplicity static values are often used, commonly used ones are shown below:
| Type of resistance | External | Internal, floor | Internal, wall | Internal, roof |
| R-value | 0.04 | 0.10 | 0.13 | 0.17 |
The formula for calculation the total R-value for practical applications therefore looks like the one below:
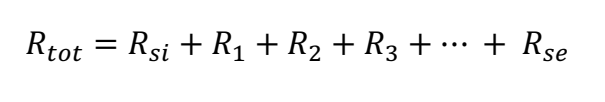
Example 3: Joey realised he did not account for the internal and external surface resistance in his calculations and wants to correct this. What are the new R-values of the walls, with and without insulation? Was the difference significant?
Answer: The wall benefits with an additional 0.13 in internal resistance and 0.04 in external resistance for a total of 0.17. The uninsulated wall therefore receives an R-value of 0.2+0.17=0.37 while the insulated wall receives an R-value of 1.45+0.17=1.62. By not accounting for these factors before Joey realised his initial calculation for the uninsulated wall was off by 85%, which is very significant, while they were off by 12% for the insulated wall.
3. Material location
While materials in general adds to the total R-value an exception is if there is an airgap heavily ventilated by outdoor air. Such airgaps are common to avoid moisture issues. In the presence of such an airgap the materials on the exterior of the airgap are not considered to add to the total R-value. The reason is that the temperature of the airgap becomes equal or near equal to that of the outside air as it is constantly being replaced.
It is important to remember that the λ-values on materials are based on certain conditions and that there are factors in the real world that can be different. The real thermal performance of a material is affected by factors such as density of the material, moisture content, the rate of convection over or through the material as well as temperature of the material. Other factors such as workmanship and building design also plays a key role in how the final construction performs. There is always a gap between the energy performance based on calculations or simulations and the real energy performance.
U-value
Before continuing it is worth mentioning that heat transfer through the construction is not the only source of heat losses in a building. Heat losses occur mainly from three areas, listed below, where this post will focus on explaining the first source of heat loss, losses through the building envelope due to heat transfer. The goal is to keep things brief and simple without going into too much detail. The three main areas of heat loss previously mentioned are:
- 1. Losses due to heat transfer through the climate envelope, i.e. the floor, walls, windows, doors and roof of the building.
- 2. Losses through the ventilation system as warm exhaust air exits the building and needs to be replaced with outdoor air.
- 3. Losses due to infiltration, meaning uncontrolled ventilation which occurs as the building is not completely airtight.
The U-value describes the thermal transmittance of the construction. The U-value takes into account heat transfer through conduction, convection and radiation. The U-value is dependent on the construction materials insulating properties, the thickness of the construction, and construction type. The U-value is calculated using the following formula:
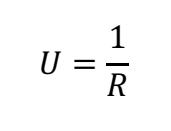
As U-value is often formed from a construction with several layers the formula can also be written as:
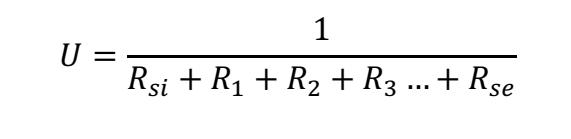
Another way of expressing it is:
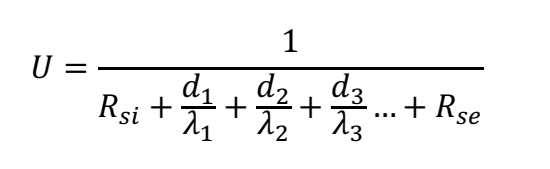
Example 4: Joey decides that he intend to build the garage with no insulation as he reckons he can always add insulation later. Remembering that the R-value of this construction was 0.37, what is the U-value?
Answer:
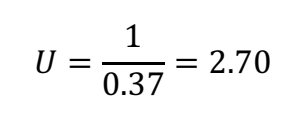
The U-value of the wall is 2.70 W/(m²K)
Bonus: Using the U-value to calculate heat transfer
The losses through the building envelope are dependent on the indoor and outdoor temperature, the U-value of the construction, and the surface area of the building. The heat transfer through a construction is described by the formula below:
Φ = Heat transfer (W)
U = Thermal transmittance of construction, U-value (W/m²K)
A = Area (m²)
ΔT = Temperature difference between indoors and outdoors (°K)
Example 5: Joey wants to keep his garage above freezing point in the winter, despite not adding any insulation. Joeys garage measures 8×5 meters and the walls are 2.5 meters high. In the front there is a garage door measuring 2.5×2 meters. What is the heat transfer through the construction if the walls have a U-value of 2.70 and the garage door have a U-value of 1.2? The outdoor temperature is -15 °C and Joey keeps the indoor temperature at 5 °C?
Answer:
The surface area of the garage wall and door is 8x5x2.5=100 m² while the door has an area of 2.5×2=5 m². This means the wall has an area of 100-5=95 m².
Method 1:
A-Wall = 95 m²
A-Door = 5 m²
ΔT = 5–(-15) = 20 °K
Φ-Wall = 95*2.7*20 = 5130 W
Φ-Door = 5*1.2*20= 120 W
Φ = Φ-Wall + Φ-Door = 5130 + 120 = 5250 W
Method 2:
Φ = U-average*A* ΔT
U-average = (2.7*95/100) + (1.2*5/100) = 2.625 W/m²K
Φ = 2.625*100*20 = 5250 W
Both methods reaches the same result. In the first method it is possible to see which part of the construction is contributing the most to the total heat transfer which is useful. The second answer instead calculate an average U-value which can be useful as a measure on how energy efficient a buildings envelope is. Regulations may set a requirement to be below a certain average U-value. The heat transfer is only specific to one point in time, in the example when its -15 outside and +5 inside. By using the minumum expected outdoor temperature the size of the heating system can be decided. This concludes this post on U-value, R-value, λ-value and heat transfer.

